Sự tồn tại của tỷ lệ vàng không chỉ để định nghĩa cái đẹp, hiện tại ngày càng có nhiều nghiên cứu khoa học phát hiện ra rằng, sự tồn tại của nó mang một ý nghĩa sâu xa hơn.
Tỷ lệ vàng trong cơ thể con người
Vào năm 2012, đài truyền hình ITV của Anh đã tổ chức cuộc thi “Gương mặt hoàn hảo Anh quốc”. Yêu cầu rất đơn giản, thí sinh chỉ cần cung cấp một bức ảnh thuần tự nhiên, không qua trang điểm, chỉnh sửa là được. Sau khi các ảnh dự thi được tổ chuyên môn lựa chọn, quán quân sẽ do công chúng bình chọn. Cuộc thi đã thu hút hơn 8,000 người tham gia. Cuối cùng, Florence Colgate, một nữ sinh 18 tuổi, đã vượt lên dẫn đầu và giành giải nhất.
Ngay khi cuộc thi có kết quả, bức ảnh quán quân này đã nhanh chóng nổi tiếng khắp thế giới. Tất cả mọi người đều khen ngợi, đây quả thực là khuôn mẫu cho một khuôn mặt hoàn mỹ.
Ngay cả cộng đồng khoa học cũng tham gia cuộc vui, nghiên cứu xem tại sao cô gái ấy lại trông xinh đẹp đến vậy.
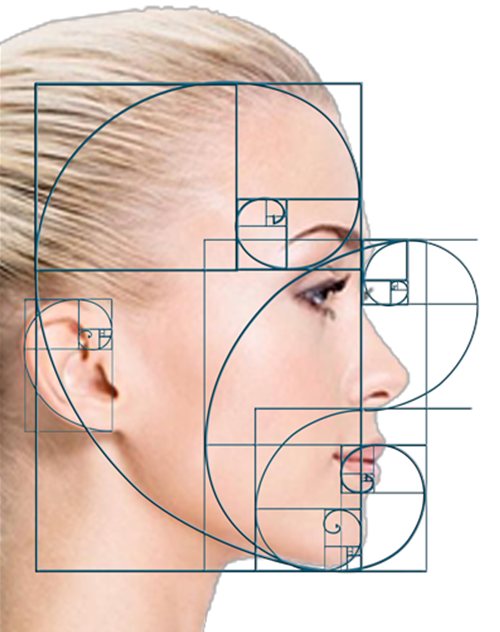
Kết quả là, các nhà nghiên cứu phát hiện ra rằng đó là một khuôn mặt rất phù hợp với tỷ lệ vàng. Có tới 24 vị trí trên khuôn mặt của Florence Colgate đạt tỷ lệ vàng. Ví dụ, tỷ lệ chiều dài so với chiều rộng của đầu, tỷ lệ từ mắt và giữa môi đến cằm, tỷ lệ từ lông mày, đường viền môi trên đến cằm, v.v.
Tỷ lệ vàng còn được gọi là tỷ lệ phân chia vàng. Chia một sợi dây thành hai đoạn, đoạn dài hơn là A và đoạn ngắn hơn là B, khi tỷ lệ giữa tổng chiều dài A + B với A bằng tỷ lệ giữa A và B thì tỷ lệ này chính là tỷ lệ vàng. Về mặt toán học, nó bằng 1 cộng với căn bậc hai của 5 rồi chia cho 2. Thông thường chúng ta lấy bốn chữ số đầu tiên là 1.618.
Người ta tin rằng, con người đã biết đến và sử dụng tỷ lệ vàng từ thời Hy Lạp cổ đại. Bằng chứng quan trọng nhất là đền Parthenon, được xây dựng vào thế kỷ thứ 5 trước Công nguyên. Không chỉ tỷ lệ bề ngoài của ngôi đền giống với tỷ lệ vàng, mà còn có thể nhìn thấy dấu vết của tỷ lệ vàng ở khắp mọi nơi trong các cấu trúc và chi tiết khác của nó. Sau đó, cộng đồng toán học đã đặt tên cho tỷ lệ vàng theo tên của nhà điêu khắc và kiến trúc đương thời Phidias, người đã tham gia thiết kế xây dựng ngôi đền. Tỉ lệ vàng từ đó được gọi là Phi, chữ Hy Lạp là Φ.
Trong hàng ngàn năm, tỷ lệ vàng đã được các nghệ sĩ vô cùng yêu thích, nó đã xuất hiện trong rất nhiều tác phẩm và xuyên suốt qua các thời đại. Nổi tiếng nhất trong số này là bức tranh “Người Vitruvius” (Vitruvian Man) của Leonardo da Vinci. Nếu bức ảnh của cô gái Florence Colgate là hiện thân của khuôn mặt người hoàn hảo nhất, thì bức tranh này của Leonardo da Vinci là hiện thân cho cơ thể con người hoàn hảo nhất, với tỷ lệ vàng ở khắp mọi nơi. Chẳng hạn, lấy rốn làm điểm phân chia, thì tỷ lệ vàng là tỉ lệ giữa thân trên và thân dưới; Lấy hầu kết làm điểm phân chia, thì tỷ lệ vàng là tỉ lệ giữa hầu đến đỉnh đầu và hầu đến rốn; Ngoài ra còn tỷ lệ giữa bàn tay so với cẳng tay; Tỷ lệ giữa chiều dài với chiều rộng lòng bàn tay, v.v.
Mặc dù đây là thân hình lý tưởng của con người, nhưng tỷ lệ cơ thể của người bình thường chúng ta nói chung là tương đương như vậy. Ngay cả hàm răng của chúng ta cũng được cấu tạo theo tỷ lệ vàng, chẳng hạn như tỷ lệ chiều rộng và chiều cao của hai răng cửa với nhau, tỷ lệ giữa răng cửa và răng kế cận, … đều gần với tỷ lệ vàng.
Vì vậy, người ta thường nói cơ thể con người là kiệt tác hoàn hảo nhất của Thượng Đế, câu nói này dường như không có gì là vô lý.
Kim tự tháp, Mặt trăng và Trái đất
Sự tồn tại của tỷ lệ vàng không chỉ để định nghĩa cái đẹp, hiện tại ngày càng có nhiều nghiên cứu khoa học phát hiện ra rằng, sự tồn tại của nó mang một ý nghĩa sâu xa hơn.
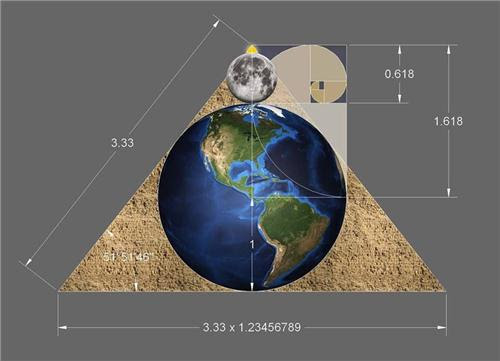
Ví dụ, giữa Mặt trăng và Trái đất cũng có tỷ lệ vàng. Trái đất có bán kính 6,378 km còn Mặt trăng có bán kính 1,736 km, tổng bán kính của cả hai là 8,114 km. Nếu coi đây là chiều cao và bán kính Trái đất làm cạnh đáy để tạo thành một tam giác vuông, thì chiều dài cạnh huyền của tam giác vuông đó sẽ là 10,321 km. Chia cạnh huyền này cho bán kính của Trái đất, kết quả chính là 1.618, là tỷ lệ vàng hoàn hảo. Đó là chưa kể, lấy bình phương của cạnh huyền chia cho bình phương của chiều cao thì cũng bằng tỷ lệ vàng hoàn hảo, 1.618.
Một tam giác như vậy có một cái tên đặc biệt là Tam giác Kepler, được đặt theo tên của nhà thiên văn học thế kỷ 17 Johannes Kepler. Tỷ lệ giữa cạnh đáy, chiều cao và cạnh huyền trong Tam giác Kepler lần lượt là 1: 1.27 : 1.618.
Và điều đáng ngạc nhiên là, cấu trúc tam giác tỷ lệ vàng này cũng xuất hiện trong kim tự tháp. Lấy Kim tự tháp Kheops làm ví dụ, đế của nó dài 215.5 mét và chiều cao là 136.4 mét. Lấy một nửa của đế là 107.8 mét làm cạnh đáy và chiều cao của tháp là 136.4 mét để tạo thành một tam giác vuông, thì chiều dài của cạnh huyền là 173.8 mét. Một phép tính đơn giản là có thể khẳng định đây cũng là một tam giác Kepler, và sai số chỉ trong vòng 1 mét.
Giữa Trái đất, Mặt trăng và kim tự tháp có mối liên hệ xảo diệu như thế nào, hiện tại chúng ta vẫn chưa thể biết. Điều thú vị là giới khảo cổ học nhìn chung đã đồng ý rằng, không có dấu hiệu nào cho thấy người Ai Cập cổ đại có kiến thức toán học về tỷ lệ vàng. Do đó, tam giác Kepler trong kim tự tháp đã trở thành một trong nhiều bằng chứng cho thấy Kim tự tháp Kheops có thể là một kiệt tác của nền văn minh thời tiền sử.
Tỷ lệ vàng trong DNA
Ông Gary Meisner, một chuyên gia về tỷ lệ vàng, đã viết trong một bài báo rằng các phân tử DNA của chúng ta đều dựa trên cơ sở là tỷ lệ vàng. Bởi vì cấu trúc hoàn chỉnh của chuỗi xoắn kép của mỗi phân tử DNA có chiều dài 34 angstrom và rộng 21 angstrom (1 angstrom có kích thước bằng 1/10 nanomet), tỷ lệ của chúng là 1.619, rất gần với tỷ lệ vàng.
DNA trong tế bào xuất hiện dưới dạng một chuỗi xoắn kép được gọi là B-DNA. Dạng DNA này có hai rãnh trong chuỗi xoắn của nó. Rãnh lớn dài khoảng 21 angstrom và rãnh nhỏ là 13 angstrom, tỷ lệ của hai con số này là 1.615, cũng rất gần với tỷ lệ vàng.
Tiến sĩ Robert Langridge, người tiên phong trong lĩnh vực đồ họa phân tử, đã nghiên cứu cấu trúc DNA từ năm 1957. Ông đã công bố một bức ảnh vào năm 1985, trong ảnh là hình ảnh một đoạn DNA cắt ngang, cho thấy rõ ràng một hình thập giác đều. Nhưng hình thập giác này kỳ thực là được tạo thành từ hai hình ngũ giác đều, một trong số đó đã được xoay 36 độ so với cái còn lại. Do đó, mỗi vòng xoắn của chuỗi xoắn kép DNA đều có dạng hình ngũ giác đều. Mà tỷ lệ giữa đường chéo và các cạnh của ngũ giác đều này lại chính xác là tỷ lệ vàng.
Vì vậy, Tiến sĩ Meisner chỉ ra rằng, dù từ góc độ nào mà xét thì DNA cũng được tạo ra theo tỷ lệ vàng. Có lẽ điều này cũng giải thích tại sao cấu trúc tỷ lệ vàng có ở khắp mọi nơi trên cơ thể con người. Trên thực tế, tỷ lệ vàng có rất nhiều trong thế giới sinh vật. Ví dụ: tỷ lệ giữa chiều dài và chiều rộng khuôn mặt của một con hổ, cũng như tỷ lệ giữa ngũ quan ở trên khuôn mặt, tỷ lệ giữa hai đôi cánh của một con bướm, tỷ lệ giữa mắt, mỏ, cánh và các vị trí quan trọng khác trên cơ thể của chim cánh cụt đều xấp xỉ tỷ lệ vàng.
Tỷ lệ vàng trong lỗ đen
Điều đáng kinh ngạc hơn nữa là tỷ lệ vàng Phi (Φ) thậm chí còn xuất hiện trong các lỗ đen. Ví dụ, Φ là điểm tới hạn mà tại đó nhiệt lượng riêng của lỗ đen chuyển từ dương sang âm, được mô tả bằng công thức sau: M 4 / J 2 = Φ
Nó cũng là một phần của phương trình giới hạn dưới của entropy lỗ đen: 8πSl2P / ekA = Φ
Nó thậm chí còn liên hệ với tham số hấp dẫn lượng tử vòng và entropy của lỗ đen: 2πγ = Φ
Cơ thể con người, sự sống, vũ trụ, nơi nào cũng đều có thể nhìn thấy bóng dáng của tỉ lệ vàng. Đó là lý do tại sao một số người nói rằng tỷ lệ vàng là mật mã của Thượng Đế.
Dãy Fibonacci
Ngoài Φ, trong “gia tộc” tỷ lệ vàng còn có một thành viên bí ẩn khác chính là dãy Fibonacci, trông giống như sau:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987……
Nó nhìn có vẻ lộn xộn và bất thường? Trên thực tế, quy tắc rất đơn giản, đó là bắt đầu từ 0 và 1, mỗi số tiếp theo là tổng của hai số trước đó. Dãy số này được nhà toán học người Ý Leonardo Fibonacci giới thiệu với mọi người trong cuốn “Sách tính toán” (The Book of Calculation) xuất bản năm 1202, và được đặt theo tên của ông. Khi các số trên dãy số ngày càng lớn thì tỷ lệ của hai số trước sau sẽ càng gần với tỷ lệ vàng. Do đó, dãy Fibonacci còn được gọi là dãy tỷ lệ vàng.
Nếu vẽ các hình vuông với các số trong dãy là độ dài cạnh, sau đó ghép chúng lại với nhau như trong hình trên, rồi vẽ một cung tròn nối 2 đỉnh đường chéo của các hình vuông lại với nhau, bạn sẽ có thể vẽ ra một hình xoắn ốc đẹp mắt. Đừng đánh giá thấp dãy số và hình xoắn ốc này, chúng cũng là một sự kết hợp rất kỳ diệu.
Ví dụ như thiết kế logo của Appl được lưu hành rộng rãi trên Internete. Đường cong của quả táo là do các vòng tròn có kích thước khác nhau tạo thành, với đường kính lần lượt là 1, 3, 5, 8, 13, v.v., tất cả đều nằm trong dãy Fibonacci. Đây là nguyên nhân tại sao quả táo này bị cắn mất một miếng nhưng trông vẫn đẹp mắt.
Trong tự nhiên, số lượng cánh hoa trong hầu hết các bông hoa đều bắt nguồn từ một số trong dãy Fibonacci. Ví dụ, hoa loa kèn có 3 cánh, hoa mai có 5 cánh, hoa phi yến có 8 cánh, cúc vạn thọ có 13 cánh, hoa hướng dương có 21 hoặc 34 cánh, hoa cúc có 34, 55 hoặc 89 cánh.
Mà hình xoắn ốc Fibonacci như trên, cũng được gọi là đường xoắn ốc vàng, nó còn được sử dụng rộng rãi hơn. Ví như khi hoa rụng và kết trái, rất nhiều hạt giống cây trồng sẽ được sắp xếp gần với đường xoắn ốc Fibonacci. Cách sắp xếp này cho phép các hạt được sắp xếp hợp lý, không bị chen chúc quá nhiều ở trung tâm và thưa thớt ở xung quanh. Một ví dụ rất điển hình là hoa hướng dương. Có người nói rằng đây là tác phẩm kỳ diệu của tự nhiên, tất cả mọi thứ đều phát triển một cách trật tự trong im lặng.
Ngoài ra, cô gái Florence Colgate với khuôn mặt đẹp hoàn hảo, khuôn mặt của cô cũng khớp vào hình xoắn ốc này, cho nên độ cong của khuôn mặt rất đẹp.
Và cả hình dạng đôi tai của chúng ta, cũng rất phù hợp với hình xoắn ốc này.
Điều bất ngờ hơn nữa là các cơn lốc xoáy cũng như các tinh vân đang quay trong Dải Ngân Hà, tất cả đều trùng khớp một cách xảo diệu với đường xoắn ốc Fibonacci.
Từ hoa hướng dương cho đến đôi tai người, từ lốc xoáy cho đến các tinh vân xa xôi, tất cả đều có hình dạng giống nhau, đây chẳng phải là điều rất thần kỳ? Tất cả những điều này có thực sự chỉ là một sự trùng hợp? Hay tất cả đều đã được Sáng Thế Chủ thiết kế một cách tỉ mỉ?
Cho đến nay, giới khoa học vẫn chưa có đáp án cuối cùng về con số tưởng chừng như rất bình thường nhưng vô cùng kỳ diệu này.
Phù Dao & Lý Duy Chân _ Xuân Hoàng
Beauty of mathematics & Numbers
| Toán Học # 1( Mathematics ) |
| Toán Học # 2 ( Mathematics ) |
| Toán Học # 3 ( Binary Math ) |
| Toán Học # 4 ( Mathematics ) |
| Toán Học và Những Con Số...Mathematics & Numbers |



















No comments:
Post a Comment
Note: Only a member of this blog may post a comment.